Model 3D Shepp-Logan w Pythonie
W dzisiejszym wpisie chciałam przybliżyć Wam, jak zaprogramować trójwymiarowy model Shepp-Logana, którego później można użyć jako obiektu rekonstrukcyjnego i rekonstruować go warstwa po warstwie. Niestety z powodu tego, że mój doktorat nie ma statusu obronionego mogę tylko umieścić kod dotyczący samego modelu, a nie algorytmu rekonstrukcyjnego.
Wprowadzenie do fantomu Shepp-Logana
Fantom Shepp-Logan składa się z kilku eliptycznych sekcji, które mogą symulować różne gęstości i struktury, takie jak kości, tkanki miękkie lub puste przestrzenie wewnątrz ludzkiego ciała. Każda elipsa w fantomie ma określone parametry, takie jak położenie, orientacja, rozmiar i współczynnik pochłaniania, co pozwala wiernie naśladować sposób, w jaki promieniowanie rentgenowskie jest pochłaniane przez różne typy tkanek.
W przestrzeni trójwymiarowej będzie on wyglądał jak na następującym obrazie (Rys. 1).
Rys. 1 Rozkład elips w trójwymiarowym
modelu Shepp-Logana
modelu Shepp-Logana
Zatem widzimy, że z trójwymiarowego modelu będziemy pozyskiwać tylko dwuwymiarowe rzuty. Model "tniemy" przez środek. W istocie w tym rzucie pozbywamy się dwóch elips, które pojawią się w innym plastrze. Najpierw model został pocięty wzdłuż osi z=-0.25. W przypadku z=0 uzyskamy inny przekrój, ale o tym za chwilę.
Parametry tabeli także nieco się zmienią, bo dodajemy parametr c i oś z do naszego układu. Dodatkowo, w przypadku niektórych elips zmieni też się odcień szarości, co musimy uwzględnić w naszej tabeli (Rys. 2).
Rys. 2 Parametry dla fantomu 3D Shepp-Logan
ellipsoid_params = [
(0.000, 0.000, 0.000, 0.6900, 0.9200, 0.9000, 0.0, 2.0), # I
(0.000, 0.000, 0.000, 0.6624, 0.8740, 0.8800, 0.0, -0.98), # II
(-0.220, 0.000, -0.250, 0.4100, 0.1600, 0.2100, 108.0, -0.02), # III
(0.220, 0.000, -0.250, 0.3100, 0.1100, 0.2200, 72.0, -0.02), # IV
(0.000, 0.350, -0.250, 0.2100, 0.2500, 0.5000, 0.0, 0.02), # V
(0.000, 0.100, -0.250, 0.0460, 0.0460, 0.0460, 0.0, 0.02), # VI
(-0.080, -0.650, -0.250, 0.0460, 0.0230, 0.0200, 0.0, 0.01), #VII
(0.060, -0.650, -0.250, 0.0230, 0.0460, 0.0200, 90.0, 0.01), # VIII
(0.060, -0.105, 0.625, 0.0400, 0.0560, 0.1000, 90.0, 0.02), # IX
(0.000, 0.100, 0.625, 0.0560, 0.0400, 0.1000, 0.0, -0.02) # X
]
Można wprowadzić parametry bardziej uniwersalnie, ale myślę, że na tym etapie będzie to wystarczające.
Istotne równania znajdjują się na Githubie i w literaturze pomocniczej [1].
Czym są te "plastry"?
Plaster lub plasterek odnosi się do dwuwymiarowego obrazu, który reprezentuje cienki przekrój skanowanego ciała lub obiektu. Skanery CT wytwarzają wiele przekrojów lub obrazów, które można następnie zrekonstruować w celu utworzenia trójwymiarowej reprezentacji skanowanego obszaru. Przekroje te są niezbędne do szczegółowej analizy i diagnostyki w obrazowaniu medycznym.
Przyjrzyjmy się zatem fragmentowi kodu, który jest odpowiedzialny za wybór plastrów (ta część nie obejmuje tutorialu, ale dowiecie się jak tę część kodu połączyć z późniejszą rekonstrukcją).
z_slice=-0.25
slice_image = generate_slice(ellipsoid_params, s_values, t_values, z_slice)
plt.imshow(slice_image, cmap='gray', extent=[min(s_values), max(s_values),
max(t_values), min(t_values)])
plt.title(f'Slice at Z={z_slice}')
plt.axis('off')
plt.show()
Zauważmy, że przypisaliśmy wartość z=-0.25, która w istocie tnie nam model nie bezpośrednio w punkcie 0, tylko -0.25. Wynika to z tego, że w punkcie zero znajdzie się tylko przekrój elipsy nr 5. Wszystkie struktury trójwymiarowe są nieco przesunięte na układzie współrzędnych (Rys. 3).
Rys. 3 Rozmieszczenie obiektów trójwymiarowych
w matematycznym modelu głowy Shepp-Logana
w matematycznym modelu głowy Shepp-Logana
Zatem jeśli chcemy dać z=0 ujrzymy tylko przeciętą kulę, która odpowiada elipsie nr 5. Przyjrzyjmy się pierwszemu przypadkowi, czyli z=-0.25 (Rys. 4).
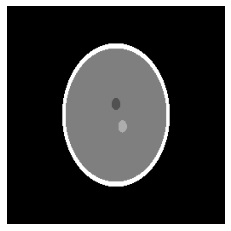
Rys. 4 Przekrój w punkcie z=-0.25
Jak widzimy nieco różni się on od fantomu Shepp-Logan w przestrzeni dwuwymiarowej, bo tak jak wspomniałam, nie mamy tutaj dwóch elips, które znajdą się w innym plastrze. Wykonamy teraz przekrój dla z=0, zmieniając wartość przy z_slice (Rys. 5).
Rys. 5 Przekrój w punkcie z=0
Widać różnicę? No dobrze, teraz zajmiemy się ostatnim krokiem, czyli uzyskaniem plastra z elipsami 9 i 10, które zabrakło nam plastrze, czyli punkcie przecięcia z=-0.25 (Rys. 6).
Rys. 6 Przekrój w punkcie z=0.625
Przeliczanie projekcji
Zwykle danych projekcyjnych pozyskuje się w plików DICOM, którego standard wchodzi w skład systemu PACS. Moja funkcja oblicza, czy punkt, po przekształceniu przez obrót i translację, mieści się w określonym wycinku elipsoidy. Wartość zwracana zależy od tego, czy punkt znajduje się wewnątrz czy na zewnątrz wycinka elipsoidy.
Krótko mówiąc, musimy sobie obraz wyrysować, czyli ten dla z=-0.25. Używamy danych projekcyjnych, które znajdują się w ellipsoid_params.
def calculate_projection_xy(x0, y0, z0, a, b, c, omega, mu, x, y, index):
omega_radians = np.radians(omega)
# Obrót punktu (x, y) wzgledem srodka ukladu wspolrzednych
x_rot = y
y_rot = -x
# Obrót punktu (x_rot, y_rot) do układu współrzędnych elipsy
if index in [3, 4]:
omega_radians = -omega_radians
if index in [8, 9]:
omega += 90
if index in [8, 9, 10]:
omega_radians -= np.pi / 2
x_dim = (x_rot - x0) * np.cos(omega_radians) -
(y_rot - y0) * np.sin(omega_radians) + x0
y_dim = (x_rot - x0) * np.sin(omega_radians) +
(y_rot - y0) * np.cos(omega_radians) + y0
# Sprawdzenie, czy punkt znajduje się wewnątrz elipsy
value = ((x_dim - x0)**2 / a**2) + ((y_dim - y0)**2 / b**2)
# Zwrócenie wartości mu jeśli punkt znajduje się wewnątrz elipsy
return mu if value <= 1 else 0
Wyróżnić możemy tutaj następujące funkcjonalności:
- konwertujemy kąt obrotu omega ze stopni na radiany,
- obracamy punkt (s, t) wokół osi z o kąt omega,
- funkcja dokonuje translacji obróconego punktu, aby można go było porównać z elipsoidą wyśrodkowaną w punkcie początkowym,
- funkcja sprawdza, czy przekształcony punkt znajduje się wewnątrz elipsoidy
return mu if value <= 1 else 0
Następnie tworzymy funkcję do przeliczania projekcji.
def calculate_projection(plane, ellipsoid_params, s_values, t_values):
projection_grid = np.zeros((image_size, image_size))
for i, s in enumerate(s_values):
for j, t in enumerate(t_values):
for index, (x0, y0, z0, a, b, c, omega, mu) in
enumerate(ellipsoid_params, start=1):
if plane == 'xy' and index not in [9, 10]:
mu_value = calculate_projection_xy(x0, y0, z0,
a, b, c, omega, mu, s, t, index)
projection_grid[i, j] += mu_value
return projection_grid
Funkcja calculate_projection służy do obliczania rzutu wielu elipsoid na płaszczyznę. W kontekście fizycznym może to reprezentować na przykład tłumienie promieniowania rentgenowskiego przechodzącego przez obiekty o różnej gęstości.
Funkcja inicjuje siatkę projection_grid w celu gromadzenia wartości. Siatka ta reprezentuje płaszczyznę, na którą będą rzutowane elipsoidy.
Następnie iteruje po wszystkich punktach (s, t) w płaszczyźnie rzutowania.
Dla każdego punktu pętla przechodzi przez każdą elipsoidę zdefiniowaną przez ellipsoid_params. Warunek if plane == 'xy' and index not in [9, 10]: sugeruje, że niektóre elipsoidy (w tym przypadku 9. i 10.) są wykluczone z rzutowania na płaszczyznę 'xy'. Oznacza to, że funkcja może obsługiwać projekcje warunkowe w oparciu o indeks elipsoidy i płaszczyznę docelową.
Funkcja okienkowania
Okienkowanie, znane również jako mapowanie poziomu szarości, rozciąganie kontrastu, modyfikacja histogramu lub wzmocnienie kontrastu, to proces, w którym składnik skali szarości obrazu TK jest manipulowany za pomocą liczb TK; spowoduje to zmianę wyglądu obrazu w celu uwydatnienia określonych struktur. Jasność obrazu jest regulowana za pomocą poziomu okna. Kontrast jest regulowany za pomocą szerokości okna.
Szerokość okna
Większa szerokość okna (2000 HU) spowoduje zatem wyświetlenie szerszego zakresu liczb TK. W związku z tym przejście ciemnych do jasnych struktur nastąpi na większym obszarze przejściowym niż w przypadku wąskiej szerokości okna (<1000 HU).
W związku z tym należy zauważyć, że znacznie szerokie okno wyświetlające wszystkie liczby TK spowoduje, że różne tłumienia między tkankami miękkimi zostaną zasłonięte.
Środek okna
Poziom okna, często określany również jako środek okna, to punkt środkowy zakresu wyświetlanych liczb TK. Gdy poziom okna zostanie zmniejszony, obraz TK będzie jaśniejszy i odwrotnie.
Chociaż różni się to nieco w zależności od instytucji i dostawcy, szerokość okna i centra są generalnie dość podobne. Wartości są zapisane jako szerokość i poziom (W:x L:y) w jednostkach Hounsfielda (HU).
Skoro trochę teorii mamy za sobą, to pora na kod.
def apply_windowing(image, level, width):
lower_bound = level - width / 2
upper_bound = level + width / 2
windowed_image = np.clip(image, lower_bound, upper_bound)
normalized_image = ((windowed_image - lower_bound) /
(upper_bound - lower_bound) * 255).astype(np.uint8)
return normalized_image
level = 1.02
width = 0.25
Musimy obliczyć górną i dolną granicę dla okienkowania. Parametr level określa punkt środkowy zakresu intensywności, a parametr width definiuje rozmiar tego zakresu. Odejmując i dodając połowę szerokości do poziomu, ustalasz zakres intensywności, który chcesz podświetlić na obrazie.
Funkcja np.clip służy do ograniczania wartości pikseli na obrazie do zakresu zdefiniowanego przez lower_bound i upper_bound. Wartości pikseli poniżej lower_bound są ustawiane na wartość lower_bound, a wartości powyżej upper_bound są ustawiane na wartość upper_bound. Ten krok skutecznie usuwa szczegóły poza oknem zainteresowania, które mogą być mniej istotne dla bieżącej analizy.
Po obcięciu intensywności w oknie są rozciągane, aby pokryć cały zakres 8-bitowej skali szarości (0-255). Okienkowany obraz jest odejmowany przez dolną granicę, która ustawia najniższą intensywność na 0. Następnie jest dzielony przez zakres (upper_bound - lower_bound), aby znormalizować te wartości do zakresu 0-1. Na koniec wynik jest mnożony przez 255, aby przeskalować go do pełnego 8-bitowego zakresu.
Funkcja zwraca normalized_image, który teraz podkreśla struktury w pierwotnie określonym oknie, jednocześnie zmniejszając lub eliminując szczegóły poza tym oknem.
Dlaczego stosujemy funkcję okienkowania? Dlatego, że różne tkanki w ciele pochłaniają promieniowanie rentgenowskie w różny sposób, a bez okienkowania rozróżnienie tkanek o podobnej charakterystyce pochłaniania może być trudne. Dostosowując poziom i szerokość, radiolodzy mogą wyróżnić różne tkanki, takie jak kości lub tkanki miękkie, aby pomóc w diagnozie.
Wyświetlanie obrazu
Kończymy z tym programem. No może nie dosłownie. Musimy wygenerować obraz!
projections = [calculate_projection(plane, ellipsoid_params, s_values, t_values)
for plane in ['xy', 'yz', 'xz']]
adjusted_projection_xy = apply_windowing(projections[0], level, width)
plt.imshow(adjusted_projection_xy, cmap='gray')
plt.show()
Uzyskaliśmy taki obraz.
Proste? Tak, pod warunkiem, że zrozumiemy cały cykl generowania modelu na podstawie parametrów. Pamiętaj, że to dopiero początek. Model jest dobrym początkiem, jeśli chcemy zaprojektować algorytm rekonstrukcyjny, np. FDK.
Podsumowanie
Jak widać, możliwe jest zaprojektowanie takiego fantomu nawet w języku Python, nie potrzeba do tego celu silnego języka programowania. Oczywiście nie mówię, że Python jest słaby. Jednakże przyzwyczailiśmy się do "ciężkich" języków programowania. Z reguły jeśli coś jest łatwe do zrobienia, to na pewno jest to kiepskie rozwiązanie.
Python szczególnie dobrze nadaje się do tego rodzaju symulacji z kilku powodów. Python posiada bardzo dobre biblioteki numeryczne, jak na przykład NumPy, która zapewnia solidne struktury do obsługi dużych zbiorów danych i macierzy, a także funkcje do wydajnego wykonywania złożonych operacji matematycznych. Python oferuje różne biblioteki, takie jak Matplotlib i Seaborn do wizualizacji danych, które mogą być pomocne w analizie i prezentacji wyników symulacji. Akurat tu nie używam Seaborn, ale na pewno sięgnę po nią jak będę generowała więcej wykresów. No i najważniejsze, Python ma stosunkowo łagodną krzywą uczenia się i jest szeroko stosowany w obliczeniach naukowych, co czyni go dobrym wyborem do opracowywania symulacji, które mogą być używane lub modyfikowane przez zespół o różnych umiejętnościach programistycznych.
No i właśnie o takich obliczeniach numerycznych też planuję wystąpienie na XV Warszawskich Dniach Informatyki.
Kod do całego modelu: https://github.com/jolapodolszanska/3D-shepp-logan-phantom
Powodzenia w Twojej przygodzie z programowaniem!
Literatura
[1] Robert Cierniak (2011), X-Ray Computed Tomography in Biomedical Engineering, Springer, ISBN: 9780857290267
[2] Carvalho, Bruno & Herman, Gabor. (2003). Helical CT Reconstruction from Wide Cone-Beam Angle Data Using ART.. 363-370. 10.1109/SIBGRA.2003.1241031.
[3] Zatz, L.M., 1981. Basic principles of computed tomography scanning. In: T.H. Newton, D.G. Potts, (Eds.), Technical Aspects of Computed Tomography. Mosby, St. Louis, pp. 3853-3876.
[4] Euclid Seeram. Computed Tomography. ISBN: 9780323312882
[5] Hoang JK, Glastonbury CM, Chen LF, Salvatore JK, Eastwood JD. CT mucosal window settings: a novel approach to evaluating early T-stage head and neck carcinoma. AJR. American journal of roentgenology. 195 (4): 1002-6. doi:10.2214/AJR.09.4149 - Pubmed








Komentarze
Prześlij komentarz